
All or Nothing (AON) AssignmentTrip Assignment
All or Nothing Assignment
Theory
IntroductionThe simplest route choice and assignment method is All-or-nothing assignment. This method assumes that there are no congestion effects, that all drivers consider the same attributes for route choice and that they perceive and weigh them in the same way. The absence of congestion effects means that link cost are fixed; the assumption that all drivers perceive the same costs means that every driver from i to j must choose the same route. Therefore, all drivers are assigned to one route between i and j and no driver is assigned to other, less attractive, routes. These assumptions are probably reasonable in sparse and uncongested networks where there are few alternative routes and they are very different in cost.
The assignment algorithm itself is the procedure that loads the matrix T to the shortest path trees and produces the flows VA, B on links (between nodes A and B). All load algorithms start with an initialization stage, in this case making all VA, B = 0 and then apply one of two basic variations: pair-by-pair methods and once -through approaches..
Example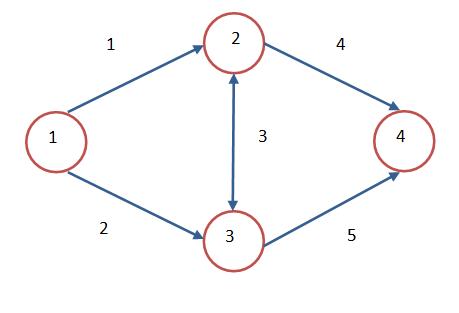
- t1=10 units
- t2=15 units
- t3=5 units
- t4=20 units
- t5=30 units
For origin: 1 destination: 2 Flow: 100 Possible path Travel Time Shortest path 1-2 10 1-2 Flow on link 1 = 100 For origin: 1 destination: 3 Flow: 200 Possible path Travel Time Shortest path 1-3 15 1-3 Flow on link 2 = 200 For origin: 1 destination: 4 Flow: 500 Possible path Travel Time Shortest path 1-2-4 10 + 20 = 30 1-2-4 1-3-4 15 + 30 = 45 1-3-4 1-2-3-4 10 + 5 + 30 = 45 1-2-3-4 Flow on link 1 = 100 + 500 = 600 Flow on link 4 = 500 For origin: 2 destination: 3 Flow: 400 Possible path Travel Time Shortest path 2-3 5 2-3 Flow on link 3 = 400 For origin: 2 destination: 4 Flow: 300 Possible path Travel Time Shortest path 2-4 20 2-4 Flow on link 4 = 500 + 300 = 800 For origin: 3 destination: 4 Flow: 600 Possible path Travel Time Shortest path 3-4 30 3-4 Flow on link 5 = 600Flow pattern based on all or nothing assignment

References Books
- J. De D. Ortuzar and L.G. Willumsen (1996), Modelling Transport. Wiley Publications, London.
- Y. Sheffi (1985), Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods. Prentice-Hall Inc., Englewood Cliffs, New Jersey.